7. Computing the Reeb graph of a filtered simplicial complex

This notebook gives a tutorial to computing the Reeb graph from a filtered simplicial complex. We assume that this complex is given as the LowerStar class (see LowerStar documentation for details).

from cereeberus import LowerStar, ReebGraph, computeReeb

Consider the following simplicial complex with height function.

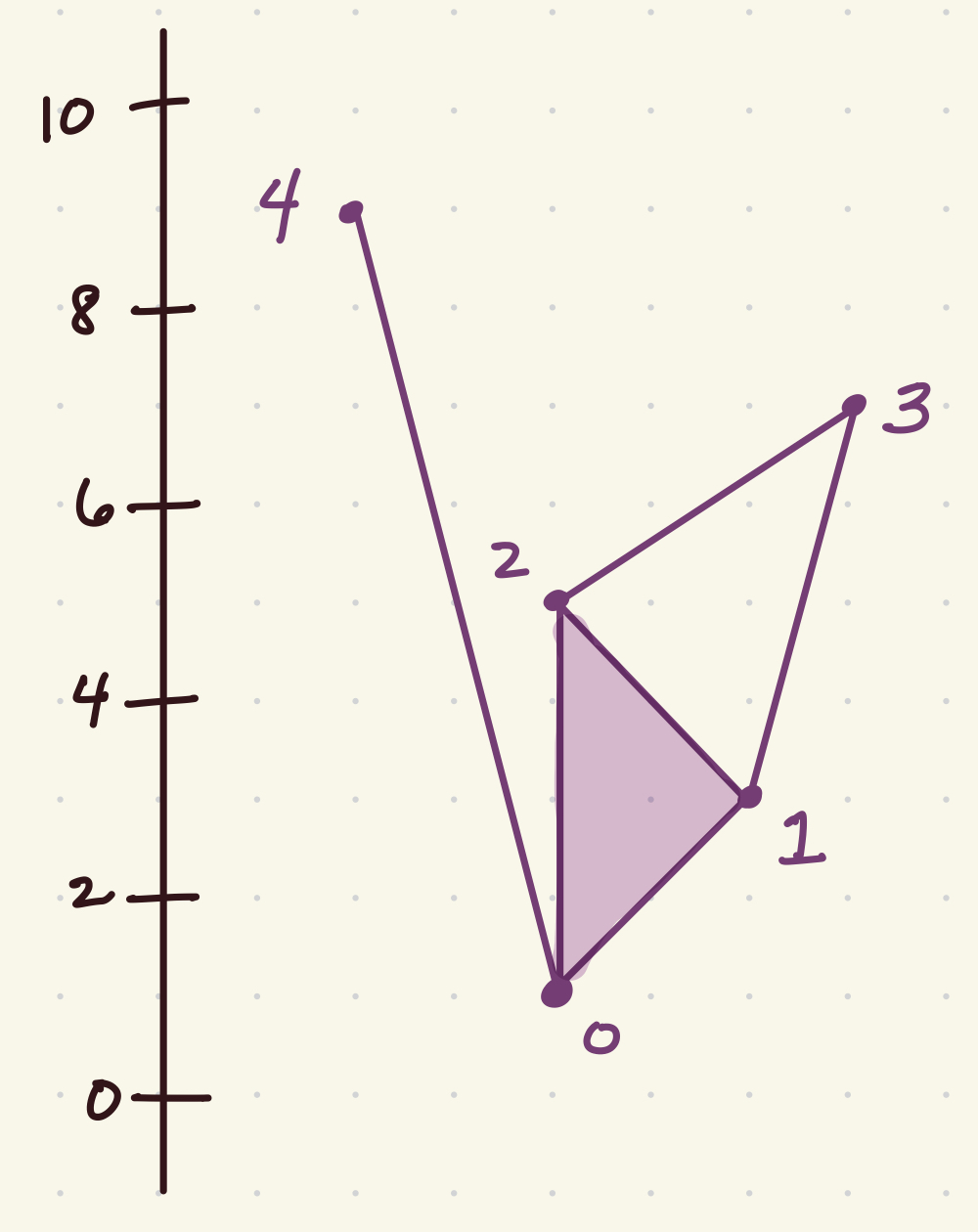
First, we construct this simplicial complex with a lower star filtration, were we need only specify the top dimensional simplices. Note that the LowerStar class is built on gudhi’s SimplexTree, so it retains all of that class’ functionality.

K = LowerStar()
K.insert([0, 1, 2])
K.insert([1, 3])
K.insert([2,3])
K.insert([0,4])
K.assign_filtration([0], 0.0)
K.assign_filtration([1], 3.0)
K.assign_filtration([2], 5.0)
K.assign_filtration([3], 7)
K.assign_filtration([4], 9.0)

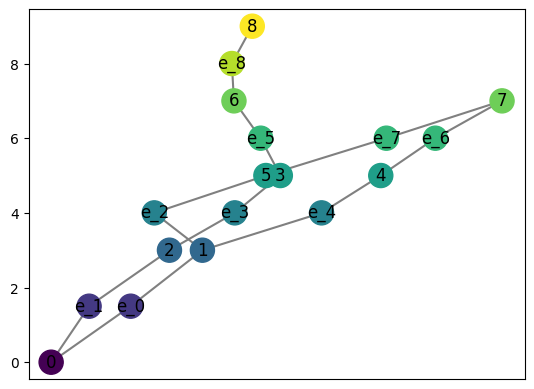
Then computing the Reeb graph of this complex is as easy as the following.

R = computeReeb(K)
R.draw()

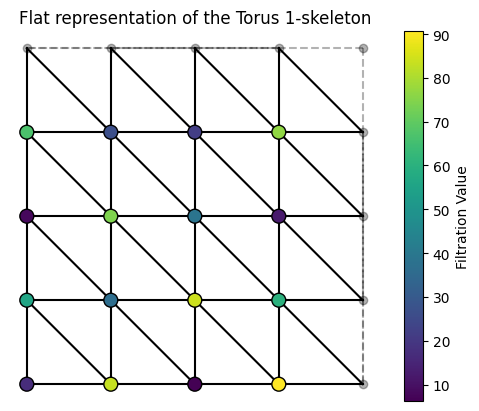
For a slightly more complex example, we have the following Torus example generator.

from cereeberus.data import Torus

T = Torus()
T.generate_grid(grid_size = 4)
T.assign_random_values(0,100, seed=1986)
T.draw()

R = computeReeb(T)
R.remove_all_regular_vertices() # Simplify for visualization

R.draw(cpx = 2)